Text Classification with Naive Bayes Classifier
Naive Bayes Classifiers are widely used in text classification problems. There are several reasons as to why they are well suited for classifying text which will be covered in this blog.
Theoretical Primer
Given a sentence S, what is the probability that it belongs to class label C? Since this is a conditional probability problem, this can be expressed as:
\[P(C | S) = \frac{P(C \displaystyle \cap S)}{P(S)}\]What if the probability of \(P(C \displaystyle \cap S)\) can’t be computed as is? We know that \(\dots\)
\[\begin{align*} P(S | C) = \frac{P(S \displaystyle \cap C)}{P(C)} \\ P(S | C)P(C) = P(S \displaystyle \cap C) \end{align*}\]and \(P(C \displaystyle \cap S) = P(S \displaystyle \cap C)\), then \(\dots\)
\[P(C \displaystyle \cap S) = P(S \displaystyle \cap C) = P(S | C)P(C)\]Now we can substitute the unknown term with terms that can be determined and arrive at Bayes’ Theorem:
\[P(C | S) = \frac{P(S|C)P(C)}{P(S)}\]What does any of this mean?
Ultimately, we want to be able to express the probability that a sentence belongs to a certain class. To do this, we also need to consider that every feature is independent from each other. Bayes’ Theorem accounts for this.
The term \(P(C)\) is commonly referred to as the “prior” and \(P(S)\) as the “evidence”. Conditional probabilites \(P(C | S)\) and \(P(S | C)\) are referred to as the “posterior” and “evidence” respectively.
\[\underbrace{P(C | S)}_\textrm{Posterior} = \frac{\overbrace{P(S|C)}^\textrm{Likelihood}\overbrace{P(C)}^\textrm{Prior}}{\underbrace{P(S)}_\textrm{Evidence}}\]How do we distinguish sentences from each other?
What makes sentences different are the words that compose a sentence and the order of those words. When order of the words matter, then this approach may not hold up. So if sentence \(S\) is just a representation of a set containing words \(w \in S\) then Bayes’ theorem becomes \(\dots\)
\[P(C | S) = \frac{P(w_{1},w_{2},\dots,w_{n}|C)P(C)}{P(w_{1},w_{2},\dots,w_{n})}\]This is where the word “Naive” is introduced because we’re naively assuming the probability of a word occurring is mutually independent from every other word. With this assumption, we can rewrite the “likelihood” as the product of probabilities for words belonging to class C:
\[P(C | S) \propto P(C)\prod_{w\in S}P(w|C)\]For a classification problem, we typically have more than one class and we’re only concerned with the class that gives us the highest probability. Since the “evidence” term remains the same for all classes, the use of \(\propto\) is used denoting proportionality. In the case of selecting the class with the highest probability, we can represent the decision rule for our prediction as:
\[\hat{y} = argmax_{c \in C} P(c)\prod_{w\in S}P(w|c)\]Naive Bayes Classifier with Python
I’ll be demonstrating my implementation of Naive Bayes Classifier for the Ford Sentence Classification Dataset. The notebook for this blog is available Here
Dataset
The dataset provides texts for job descriptions as New_Sentence and their types as Type. The goal of the classifier is to identify sentence as class type Responsibility, Requirement, Skill, SoftSkill, Education or Experience.
I split data into train, validation, and test sets below.
import pandas as pd
import re
import math
datapath = "~/Documents/datasets/ford_sentence/data.csv"
data = pd.read_csv(datapath, skip_blank_lines=True)
data = data.dropna(how="any")
size = data.shape[0]
train_data = data.loc[:int(0.6 * size)]
val_data = data.loc[int(0.6 * size):int(0.8 * size)]
test_data = data.loc[int(0.8 * size):]Building the Classifier
I’ll be showing you the process of building the Naive Bayes Classifier class I came up with.
Computing Priors
We can start with computing the prior probabilities of each class \(P(c)\) which is fairly simple. Just divide the number of occurrences for a class by the number of data samples for every class. Here’s how I did that:
def separate_by_class(self, train_data):
class_tables = {}
for type in train_data.Type:
if type not in class_tables:
class_tables[type] = train_data.loc[train_data.Type == type]
return class_tablesdef compute_priors(self, train_data):
priors = {}
for class_type, class_data in self.class_tables.items():
priors[class_type] = class_data.shape[0] / train_data.shape[0]
return priorsComputing Occurrences
Now we want to be able to have the probability for a word occuring in a specific class \(P(w|c)\). To do this, calculate the total number of times a word appears in a class and divide by the class size. Do this for every word in a class and for every class.
def compute_occurrences(self):
vocab_class = {}
for class_type, class_data in self.class_tables.items():
vocab_class[class_type] = {}
for sentence in class_data.New_Sentence:
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
for word in sentence.split():
if word in vocab_class[class_type]:
vocab_class[class_type][word] += 1
else:
vocab_class[class_type][word] = 1
omitted_vocab = {
key : 0 for key, val in vocab_class[class_type].items() if val >= 5
}
vocab_class[class_type] = omitted_vocab
for class_type, class_data in self.class_tables.items():
class_size = len(class_data.New_Sentence)
vocab = vocab_class[class_type]
for sentence in class_data.New_Sentence:
added = set()
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
for word in sentence.split():
if word in vocab.keys() and word not in added:
vocab[word] += 1
added.add(word)
for word in vocab.keys():
vocab[word] += self.alpha
vocab[word] /= (self.alpha * self.n_classes + class_size)
vocab_class[class_type] = {
k: v for k, v in sorted(
vocab.items(), key=lambda item: item[1], reverse=True
)
}
return vocab_classThe first loop is deciding which words belongs to a class (the vocabulary of a class). It will omit words that are very uncommon and characters not in the alphabet.
Second loop is doing word occurence calculations. Notice that I’m not readding words that have already shown up in a sentence because class size is defined by number of sentences rather than number of words. I will explain the use of the alpha variable later.
Computing Class Predictions
Now that we have the probabilities of a word appearing in a particular class, we can calulate the product for each word in the sentence we want to predict to get the likelihood. Then multiply the likelihood by the prior of the class to get the posterior probability. Do this for each class and take the class with the highest posterior probability as our prediction.
\[\begin{align*} \text{Recall} \quad \quad \underbrace{P(C | S)}_\textrm{Posterior} \propto \underbrace{P(C)}_\textrm{Prior}\underbrace{\prod_{w\in S}P(w|C)}_\textrm{Likelihood} \end{align*}\]def __call__(self, sentence):
max_posterior = (None, 0)
for class_type, prior in self.priors.items():
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
likelihood = prior
class_size = len(self.occurrences[class_type].keys())
for word in sentence.split():
if word in self.occurrences[class_type]:
likelihood *= self.occurrences[class_type][word]
elif self.smoothing:
likelihood *= self.alpha / \
(self.alpha * self.n_classes + class_size)
else:
likelihood *= 0
if likelihood > max_posterior[1]:
max_posterior = (class_type, likelihood)
return max_posteriorPutting Everything Together
class NBC():
def __init__(self, train_data, smoothing=True, alpha=1) -> None:
assert alpha > 0, "Alpha must be greater than 0"
self.regex = re.compile('[^a-zA-Z ]')
self.alpha = alpha
self.smoothing = smoothing
self.class_tables = self.separate_by_class(train_data)
self.priors = self.compute_priors(train_data)
self.n_classes = len(self.priors.keys())
self.occurrences= self.compute_occurrences()
def separate_by_class(self, train_data):
class_tables = {}
for type in train_data.Type:
if type not in class_tables:
class_tables[type] = train_data.loc[train_data.Type == type]
return class_tables
def compute_priors(self, train_data):
priors = {}
for class_type, class_data in self.class_tables.items():
priors[class_type] = class_data.shape[0] / train_data.shape[0]
return priors
def compute_occurrences(self):
vocab_class = {}
for class_type, class_data in self.class_tables.items():
vocab_class[class_type] = {}
for sentence in class_data.New_Sentence:
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
for word in sentence.split():
if word in vocab_class[class_type]:
vocab_class[class_type][word] += 1
else:
vocab_class[class_type][word] = 1
omitted_vocab = {
key : 0 for key, val in vocab_class[class_type].items() if val >= 5
}
vocab_class[class_type] = omitted_vocab
for class_type, class_data in self.class_tables.items():
class_size = len(class_data.New_Sentence)
vocab = vocab_class[class_type]
for sentence in class_data.New_Sentence:
added = set()
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
for word in sentence.split():
if word in vocab.keys() and word not in added:
vocab[word] += 1
added.add(word)
for word in vocab.keys():
vocab[word] += self.alpha
vocab[word] /= (self.alpha * self.n_classes + class_size)
vocab_class[class_type] = {
k: v for k, v in sorted(
vocab.items(), key=lambda item: item[1], reverse=True
)
}
return vocab_class
def __call__(self, sentence):
max_posterior = (None, 0)
for class_type, prior in self.priors.items():
sentence = sentence.lower()
sentence = self.regex.sub(' ', sentence)
likelihood = prior
class_size = len(self.occurrences[class_type].keys())
for word in sentence.split():
if word in self.occurrences[class_type]:
likelihood *= self.occurrences[class_type][word]
elif self.smoothing:
likelihood *= self.alpha / \
(self.alpha * self.n_classes + class_size)
else:
likelihood *= 0
if likelihood > max_posterior[1]:
max_posterior = (class_type, likelihood)
return max_posteriorModel Evaluation
To see how the model performs, total the number of correct predictions and compare it with the size of the validation set to get the accuracy.
def eval(model, data):
score = 0
for i in range(data.shape[0]):
pred, _ = model(data.iloc[i].New_Sentence)
score += pred == data.iloc[i].Type
return score / data.shape[0]Smoothing
model = NBC(train_data, smoothing=False)
print(f"Accuracy: {eval(model, val_data)} ")output
Accuracy: 0.37965281975991017Since the dataset has six class labels total, it appears to be doing better than just chance. However, this isn’t the performance we want. Whenever there’s a word that isn’t in a class vocabulary from the training data, the posterior probability becomes zero. We could have a pretty good prediction for a class up until there is a word that isn’t in the class. To fix this, we can incorporate Laplace Smoothing so that we’re never eliminating a prediction based on a word not occuring in the class.
without smoothing:
\[P(w|c) = \frac{0}{N} = 0\]with smoothing:
\[P(w|c) = \frac{0 + \alpha}{N + \alpha K} \quad \alpha > 0\]where N is the size of a class and K is the number of classes
model = NBC(train_data, smoothing=True)
print(f"Accuracy: {eval(model, val_data)} ")output
Accuracy: 0.6546333880300544 Using Laplace Smoothing, I was able to significantly improve the model accuracy by roughly 30%.
Analyzing class accuracies
Now that we have the overall performance of the model, let’s see how the model is performing on each class.
def class_perf(model, data):
class_performance = {}
for class_type in model.priors.keys():
class_performance[class_type] = \
eval(model, val_data[val_data.Type == class_type])
df_perf = pd.Series(class_performance)
print("Accuracy by class:")
print(df_perf)output
Accuracy by class:
Responsibility 0.882784
Requirement 0.320044
Skill 0.383171
SoftSkill 0.642973
Education 0.860045
Experience 0.898190
dtype: float64The model is not performing well for sentences of type Requirement and Skill. Looking at which words contribute the most to the prediction for the classes may give us some insight into why this is the case.
top_words = {}
for class_type, class_occ in model.occurrences.items():
top_words[class_type] = [*class_occ.keys()][:10]
top_class_words = pd.DataFrame(top_words)
top_class_words.index += 1
top_class_wordsThe values were sorted in desecending order during training, so we can just take the first ten values.
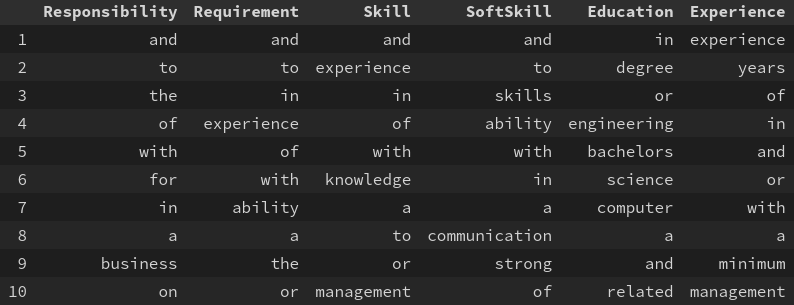
The column for the top ten words in Requirements is very similar to the column for Skill. This indicates that their is a lot overlap between the occurences for certain words in Requirement sentences and Skill sentences.
I tried messing around with one of the column values for these words to see if it improves the performance. I found that if I set some of the words in Requirements to 1, it improved the model by 3%.
import copy
model_copy = copy.deepcopy(model)
req = model_copy.occurrences["Requirement"]
ignore = ["and", "with", "in", "of", "or", "experience"]
for word in ignore:
req[word] = 1print(f"Accuracy: {eval(model_copy, val_data)} ")
class_perf(model_copy, val_data)output
Accuracy: 0.6897832282580534
Accuracy by class:
Responsibility 0.856810
Requirement 0.607169
Skill 0.311044
SoftSkill 0.572429
Education 0.838600
Experience 0.867647
dtype: float64I believe this works because it’s essentially ignoring the words when computing the likelihood. Since we do this for one of the classes, the model is able to differentiate Requirement and Skill class better.
Now let’s see if the changes we made influenced the performance on the test set.
print(f"Accuracy: {eval(model, test_data)} ")
print(f"Accuracy: {eval(model_copy, test_data)} ")output
Original Accuracy: 0.650967996839194
Modified Accuracy: 0.6809956538917424 Closing Thoughts
By using a Naive Bayes Classifier, I was able to predict six different types of sentences for the dataset with 68% accuracy. Considering all of the similarities between the different types of sentences in the dataset, I expected this performance using Naive Bayes. I was able to slightly overcome this by modifying some of the most influential words for a particular class, improving the original model by roughly 3%.